5.6. Análisis de Varianza#
El análisis de varianza es un caso especial de la regresión lineal que contesta la hipótesis alterna \( H_1: \exists\, i,j \in \{1, \dots, k\},\ i \ne j,\ \mu_i \ne \mu_j \), que se lee como: existe un par i,j en los grupos de estudio para los que las medias de la variable dependiente son diferentes.
Importante
Para esta libreta además de la librería statsmodels, utilizaremos pingouin una nueva librería que deberás instalar con uv add pingouin o pip install pingouin si no estás utilizando uv.
Considera que a diferencia de las demás librerías utilizadas hasta el momento, pingouin no está preinstalada en google colab, si estás trabajando en colab, corre lo siguiente en una celda de código:
!pip install -q pingouin
Hazlo antes de intentar importar la librería.
5.6.1. Librerías#
import pandas as pd
import scipy.stats as stats
import statsmodels.api as sm
#!pip install -q pingouin # quita el comentario si estás en colab.
import pingouin as pg
import matplotlib.pyplot as plt
import seaborn as sns
print('Librerías importadas')
Librerías importadas
5.6.2. Datos#
Para esta libreta utilizaremos el dataset palmer penguins que trabajamos en la Unidad 4, pero esta vez lo cargaremos desde pingouin.
Muchas librerías, tanto en python como en R, nos permiten importar bases de datos para probarlos. En las librerías que ya hemos utilizado, seaborn y statsmodels ofrecen muchos datos para probar, te sugiero que busques en su documentación.
data = pg.read_dataset('penguins')
data.head()
| species | island | bill_length_mm | bill_depth_mm | flipper_length_mm | body_mass_g | sex | |
|---|---|---|---|---|---|---|---|
| 0 | Adelie | Biscoe | 37.8 | 18.3 | 174.0 | 3400.0 | female |
| 1 | Adelie | Biscoe | 37.7 | 18.7 | 180.0 | 3600.0 | male |
| 2 | Adelie | Biscoe | 35.9 | 19.2 | 189.0 | 3800.0 | female |
| 3 | Adelie | Biscoe | 38.2 | 18.1 | 185.0 | 3950.0 | male |
| 4 | Adelie | Biscoe | 38.8 | 17.2 | 180.0 | 3800.0 | male |
5.6.3. Plan de análisis#
Primero haremos un ANOVA de una vía, con la variable body_mass_g como dependiente y la variable species como factor de agrupación (independiente categórica).
Lo que queremos probar es lo siguiente:
Es decir, existe un par de especies con media diferente para el peso.
Nuestro objetivo es probar la hipótesis nula:
5.6.4. Statsmodels#
Statsmodels implementa ANOVA como la extensión del modelo lineal, sin embargo, sus resultados son limitados y para obtener tamaños del efecto requeriríamos código adicional, por esto, pingouin trabaja a un mayor nivel programático, abstrayendo la tarea compleja. Primero veamos cómo generamos la tabla ANOVA con statsmodels
model_res = sm.OLS.from_formula(
'body_mass_g ~ species', data
).fit()
table = sm.stats.anova_lm(model_res)
table
| df | sum_sq | mean_sq | F | PR(>F) | |
|---|---|---|---|---|---|
| species | 2.0 | 1.468642e+08 | 7.343211e+07 | 343.626275 | 2.892368e-82 |
| Residual | 339.0 | 7.244348e+07 | 2.136976e+05 | NaN | NaN |
Vemos que podemos rechazar la hipótesis nula, pero veamos cómo se ve este análisis con pingouin.
5.6.5. Pingouin#
Esta librería fue creada como una extensión alto nivel de statsmodels y scipy y está enfocada en tamaños del efecto para uso clínico, por lo que es ideal para su uso en ciencias de la salud.
pg.anova(
data, # los datos
dv='body_mass_g', # variable dependiente
between='species', # variable de agrupación
detailed=True, # información adicional
)
| Source | SS | DF | MS | F | p-unc | np2 | |
|---|---|---|---|---|---|---|---|
| 0 | species | 1.468642e+08 | 2 | 7.343211e+07 | 343.626275 | 2.892368e-82 | 0.669672 |
| 1 | Within | 7.244348e+07 | 339 | 2.136976e+05 | NaN | NaN | NaN |
Podemos ver que con una sola función de fácil uso, logramos un resultado muy parecido pero con información adicional, muy importante np2 corresponde a \(\eta^2\), el tamaño del efecto.
Esto lo intepretamos como que existe una diferencia significativa en el peso de los pingüinos de acuerdo a su especie, con un tamaño de efecto muy grande. Visualicémoslo.
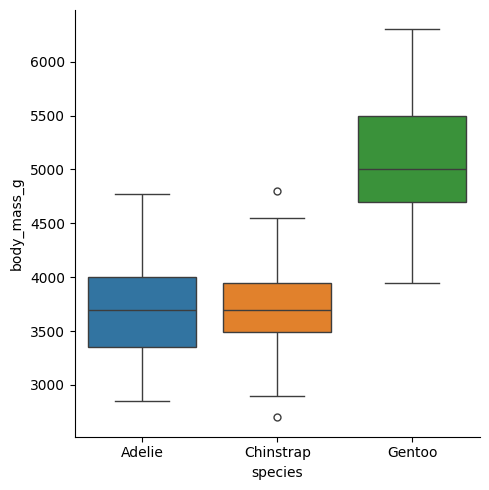
sns.catplot(
data,
x='species',
y='body_mass_g',
kind='box',
hue='species', # agrega color
)
<seaborn.axisgrid.FacetGrid at 0x1a22c18d160>
5.6.6. Post-Hoc#
Habiendo encontrado la diferencia, lo apropiado es correr una prueba post-hoc para encontrar los pares que difieren.
Pingouin ofrece esta herramienta con el código prácticamente idéntico que para el ANOVA.
pg.pairwise_tukey(
data, # los datos
dv='body_mass_g', # variable dependiente
between='species', # variable de agrupación
)
| A | B | mean(A) | mean(B) | diff | se | T | p-tukey | hedges | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | Adelie | Chinstrap | 3700.662252 | 3733.088235 | -32.425984 | 67.511684 | -0.480302 | 0.880667 | -0.073946 |
| 1 | Adelie | Gentoo | 3700.662252 | 5076.016260 | -1375.354009 | 56.147971 | -24.495169 | 0.000000 | -2.860201 |
| 2 | Chinstrap | Gentoo | 3733.088235 | 5076.016260 | -1342.928025 | 69.856928 | -19.223978 | 0.000000 | -2.875327 |
Corroboramos lo que el diagrama de caja y brazos sugería, existe una diferencia entre Gentoo y las otras dos especies, pero no entre Adelie y Chinstrap.
Observa además que tenemos el tamaño del efecto de hedge para cada par.
5.6.7. ANOVA de dos vías#
Repitamos el análisis pero ajustemos como agrupación adicional sex, para ver si el peso varía también entre sexos y si la especie puede interactuar con el sexo afectando el peso del pingüino.
pg.anova(
data,
dv='body_mass_g',
between=['species', 'sex'], # pasamos list en lugar de str
detailed=True,
)
| Source | SS | DF | MS | F | p-unc | np2 | |
|---|---|---|---|---|---|---|---|
| 0 | species | 1.434016e+08 | 2.0 | 7.170079e+07 | 749.015666 | 8.144406e-123 | 0.820825 |
| 1 | sex | 3.709026e+07 | 1.0 | 3.709026e+07 | 387.459976 | 1.902273e-57 | 0.542312 |
| 2 | species * sex | 1.676557e+06 | 2.0 | 8.382784e+05 | 8.756997 | 1.973489e-04 | 0.050837 |
| 3 | Residual | 3.130263e+07 | 327.0 | 9.572669e+04 | NaN | NaN | NaN |
Corroboramos nuevamente nuestra hipótesis, existe dimorfismo sexual. Veamos el post-hoc the tukey para sexo.
pg.pairwise_tukey(
data,
dv='body_mass_g',
between='sex',
)
| A | B | mean(A) | mean(B) | diff | se | T | p-tukey | hedges | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | female | male | 3862.272727 | 4545.684524 | -683.411797 | 80.008683 | -8.54172 | 1.612044e-13 | -0.934082 |
Y para la interacción? Para esto debemos crear una nueva variable que combine los pares entre especie y sexo y meteremos cada una dentro de la prueba de tukey.
data['group'] = data['species'] + '-' + data['sex']
# Comparaciones post-hoc entre combinaciones especie-sexo
pg.pairwise_tukey(
data=data,
dv='body_mass_g',
between='group'
)
| A | B | mean(A) | mean(B) | diff | se | T | p-tukey | hedges | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | Adelie-female | Adelie-male | 3368.835616 | 4043.493151 | -674.657534 | 51.211806 | -13.173867 | 0.000000e+00 | -2.161343 |
| 1 | Adelie-female | Chinstrap-female | 3368.835616 | 3527.205882 | -158.370266 | 64.240295 | -2.465279 | 1.376213e-01 | -0.572822 |
| 2 | Adelie-female | Chinstrap-male | 3368.835616 | 3938.970588 | -570.134972 | 64.240295 | -8.875037 | 0.000000e+00 | -1.876696 |
| 3 | Adelie-female | Gentoo-female | 3368.835616 | 4679.741379 | -1310.905763 | 54.422282 | -24.087666 | 0.000000e+00 | -4.741976 |
| 4 | Adelie-female | Gentoo-male | 3368.835616 | 5484.836066 | -2116.000449 | 53.671357 | -39.425134 | 0.000000e+00 | -7.252527 |
| 5 | Adelie-male | Chinstrap-female | 4043.493151 | 3527.205882 | 516.287268 | 64.240295 | 8.036813 | 1.999512e-13 | 1.559300 |
| 6 | Adelie-male | Chinstrap-male | 4043.493151 | 3938.970588 | 104.522562 | 64.240295 | 1.627056 | 5.812048e-01 | 0.295064 |
| 7 | Adelie-male | Gentoo-female | 4043.493151 | 4679.741379 | -636.248229 | 54.422282 | -11.690951 | 0.000000e+00 | -1.978960 |
| 8 | Adelie-male | Gentoo-male | 4043.493151 | 5484.836066 | -1441.342915 | 53.671357 | -26.854974 | 0.000000e+00 | -4.317487 |
| 9 | Chinstrap-female | Chinstrap-male | 3527.205882 | 3938.970588 | -411.764706 | 75.039869 | -5.487279 | 1.219550e-06 | -1.248653 |
| 10 | Chinstrap-female | Gentoo-female | 3527.205882 | 4679.741379 | -1152.535497 | 66.827772 | -17.246355 | 0.000000e+00 | -4.039086 |
| 11 | Chinstrap-female | Gentoo-male | 3527.205882 | 5484.836066 | -1957.630183 | 66.217679 | -29.563558 | 0.000000e+00 | -6.396393 |
| 12 | Chinstrap-male | Gentoo-female | 3938.970588 | 4679.741379 | -740.770791 | 66.827772 | -11.084775 | 0.000000e+00 | -2.342940 |
| 13 | Chinstrap-male | Gentoo-male | 3938.970588 | 5484.836066 | -1545.865477 | 66.217679 | -23.345208 | 0.000000e+00 | -4.627380 |
| 14 | Gentoo-female | Gentoo-male | 4679.741379 | 5484.836066 | -805.094686 | 56.742843 | -14.188480 | 0.000000e+00 | -2.682582 |
Podemos ver un enorme efecto entre sexo y especie, sobre todo en los machos Gentoo, que son los más pesados.
5.6.8. ANCOVA#
Para terminar las demostraciones, ajustemos el modelo simple de nuestro ANOVA de una vía entre peso y especie para el tamaño del pico.
pg.ancova(
data,
dv='body_mass_g',
between='species',
covar=['bill_length_mm', 'bill_depth_mm']
)
| Source | SS | DF | F | p-unc | np2 | |
|---|---|---|---|---|---|---|
| 0 | species | 7.828083e+07 | 2 | 349.264191 | 7.093167e-83 | 0.674562 |
| 1 | bill_length_mm | 6.633645e+06 | 1 | 59.194431 | 1.591048e-13 | 0.149408 |
| 2 | bill_depth_mm | 9.847683e+06 | 1 | 87.874461 | 1.044582e-18 | 0.206825 |
| 3 | Residual | 3.776602e+07 | 337 | NaN | NaN | NaN |
5.6.9. Medidas repetidas#
Analizaremos ahora el dataset sleepstudy que analizó a una serie de sujetos en el tiempo y cómo su tiempo de reacción se deteriora en el tiempo conforme se les depriva de sueño.
Este dataset se utiliza con mucha frecuencia en el contexto de modelos mixtos, también lo utilizaremos con ese fin más adelante en el curso, pero por ahora veamos cómo se ve el ANOVA de medidas repetidas
sleep_data = sm.datasets.get_rdataset('sleepstudy', package='lme4').data
sleep_data.head()
| Reaction | Days | Subject | |
|---|---|---|---|
| 0 | 249.5600 | 0 | 308 |
| 1 | 258.7047 | 1 | 308 |
| 2 | 250.8006 | 2 | 308 |
| 3 | 321.4398 | 3 | 308 |
| 4 | 356.8519 | 4 | 308 |
Visualicemos los cambios.
sns.lmplot(
sleep_data,
col='Subject',
col_wrap=6,
x='Days',
y='Reaction',
aspect=0.6,
)
<seaborn.axisgrid.FacetGrid at 0x1a22e3691d0>
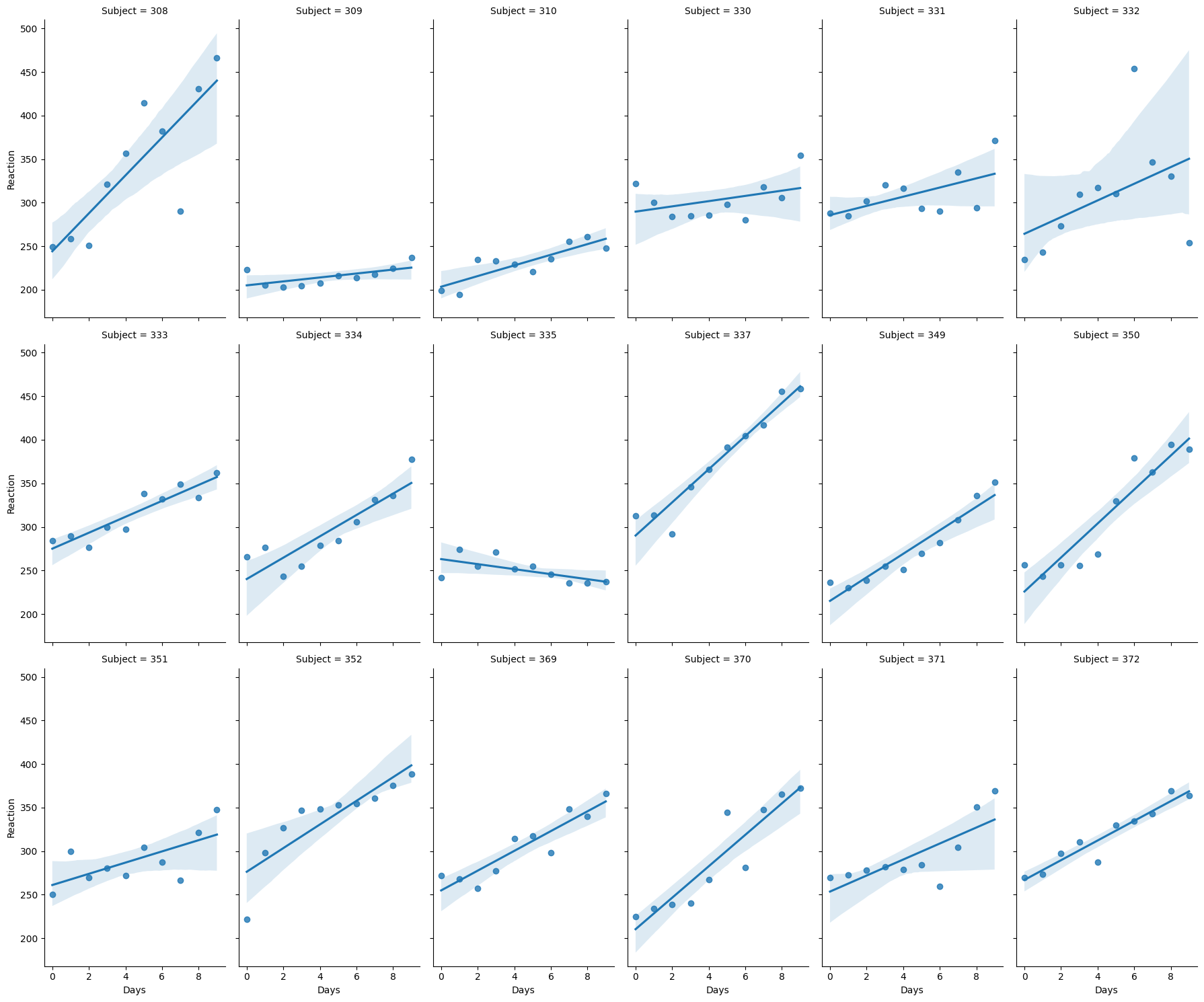
Podemos ver que en general, se incrementa el tiempo de reacción conforme se depriva del sueño al sujeto, excepto para el sujeto 335 que se tomó muy serie el ejercicio.
Probemos ahora la hipótesis de que el tiempo de reacción no varía de acuerdo al número de días.
pg.rm_anova(
sleep_data,
dv='Reaction',
within='Days',
subject='Subject'
)
| Source | ddof1 | ddof2 | F | p-unc | p-GG-corr | ng2 | eps | sphericity | W-spher | p-spher | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | Days | 9 | 153 | 18.702698 | 8.995345e-21 | 5.463092e-09 | 0.292691 | 0.36903 | False | 0.000219 | 5.154879e-08 |
Podemos ver que el tiempo efectivamente varía en el tiempo para cada sujeto, con una p significativa, aún con la corrección por esfericidad (Greenhouse-Geisser). Por lo que corroboramos que existe un cambio significativo con un tamaño de efecto importante.
5.6.10. No paramétrico#
Veamos cómo analizar la diferencia entre más de dos grupos con las pruebas no paramétricas de Kruskal-Wallis y Friedman.
5.6.10.1. Grupos independientes#
Para analizar más de dos grupos en forma no paramétrica, la prueba de rutina es Kruskal-Wallis, que en python está implementada en varios paquetes.
5.6.10.1.1. Scipy#
clean_data = data.dropna(subset=['species', 'body_mass_g'])
# esta es otra forma de extraer los grupos
# primero agrupamos y seleccionamos la columna
groups = clean_data.groupby('species')['body_mass_g']
# luego extraemos los grupos
adelie = groups.get_group('Adelie')
chinstrap = groups.get_group('Chinstrap')
gentoo = groups.get_group('Gentoo')
stats.kruskal(adelie, chinstrap, gentoo)
KruskalResult(statistic=np.float64(217.59924143680436), pvalue=np.float64(5.609512095829062e-48))
5.6.10.1.2. Pingouin#
# la sintaxis es muy parecida al anova
pg.kruskal(data, dv='body_mass_g', between='species', detailed=True)
| Source | ddof1 | H | p-unc | |
|---|---|---|---|---|
| Kruskal | species | 2 | 217.599241 | 5.609512e-48 |
5.6.10.2. Medidas repetidas#
Para el análisis de Friedman contamos con las mismas herramientas.
5.6.10.2.1. scipy#
Como tenemos varios días en el estudio, necesitamos extraer cada día directamente a un objeto, en lugar de separar en variables como hicimos con las especies, lo haremos con los días.
dias = []
for name, group in sleep_data.groupby('Days')['Reaction']:
print('guardando día:', name)
dias.append(group)
guardando día: 0
guardando día: 1
guardando día: 2
guardando día: 3
guardando día: 4
guardando día: 5
guardando día: 6
guardando día: 7
guardando día: 8
guardando día: 9
Ahora en la variable dias tenemos una lista con los valores del tiempo de reacción para cada día, pongámoslo en la prueba de friedman.
stats.friedmanchisquare(*dias)
FriedmanchisquareResult(statistic=np.float64(86.08484848484852), pvalue=np.float64(9.904181018793203e-15))
El operador * antes de la lista, «desempaqueta» la colección en los argumentos de la función. Si analizamos el encabezado de la función vemos esto def friedmanchisquare(*samples: Any), puedes ver que samples es un argumento que puede recibir cualquier cantidad de valores y terminan todos en una lista, al utilizar *dias estamos pasando cada objeto dentro de la lista al parámetro samples. Revisa el tema de argumentos para recordar estos conceptos.
5.6.10.2.2. pingouin#
pg.friedman(
sleep_data, dv='Reaction', within='Days', subject='Subject',
)
| Source | W | ddof1 | Q | p-unc | |
|---|---|---|---|---|---|
| Friedman | Days | 0.531388 | 9 | 86.084848 | 9.904181e-15 |
Nuevamente pingouin es más sencillo de utilizar y produce resultados más estéticos.
5.6.11. Ejercicios#
Explora qué otros datasets están disponibles en las tres librerías
seaborn,statsmodelsypingouin. Deberás revisar su documentación.Utiliza
statsmodelspara ejecutar las pruebas post-hoc,pingouinlo hace muy fácil, ve si puedes descifrar cómo hacerlo sin esta herramienta.Explora cómo cambiar los supuestos (por ejemplo, violación de esfericidad o heterocedasticidad) y cómo afectan los resultados del ANOVA.

