Pruebas T, parte 2

6.3. Pruebas T, parte 2#

Nota

Esta libreta es la parte 2 del análisis bayesiano de comparación de medias, pero también es la introducción para los modelos lineales

En esta libreta veremos otro método para realizar una comparación de dos medias.

Te sugiero que revises esta libreta de la documentación de bambi para mayor explicación del modelo y un ejemplo diferente.

Cuando utilizamos una prueba t, lo que hacemos es comparar dos medias en dos grupo con la hipótesis \(\mu_0 \ne \mu_1\), al hacerlo, utilizamos de forma implícita un modelo lineal, donde comparamos:

\[\mu_i = \beta_0 + \beta_1(i) + \epsilon\]

En este caso \(i\) es valor dicotómico de la población en cuestión. Retomando el dataset palmer penguins, si comparamos el peso entre la población Adelie y la Chinstrap, dentro del modelo, \(\text{adelie} = 0\) y \(\text{chinstrap} = 1\); de tal forma que \(i \in {0, 1}\). Al sustituir los índices:

\[\mu_0 = \beta_0 + \epsilon\]
\[\mu_1 = \beta_0 + \beta_1 + \epsilon\]

Por lo tanto, para el caso de la hipótesis nula \(\mu_0 = \mu_1\), la ecuación de interés es:

\[\beta_0 + \epsilon = \beta_0 + \beta_1 + \epsilon\]

Resolviendo para \(\beta_1\):

\[\beta_1 = 0\]

Repasando, en el modelo que contruiremos, la categoría de referencia es «Adelie», \(\beta_0\) es la media de peso de los Adelie y \(\beta_1\) es la diferencia de peso entre los Adelie y los Chinstrap.

6.3.1. Librerías y datos#

import bambi as bmb
import arviz as az
import pingouin as pg

data = pg.read_dataset('penguins')
data.head()
species island bill_length_mm bill_depth_mm flipper_length_mm body_mass_g sex
0 Adelie Biscoe 37.8 18.3 174.0 3400.0 female
1 Adelie Biscoe 37.7 18.7 180.0 3600.0 male
2 Adelie Biscoe 35.9 19.2 189.0 3800.0 female
3 Adelie Biscoe 38.2 18.1 185.0 3950.0 male
4 Adelie Biscoe 38.8 17.2 180.0 3800.0 male

6.3.2. Definición del modelo#

Necesitaremos la fórmula, los datos y especificaremos la familia de la distrubicón, en este caso utilizaremos la distribución T, ya que es más robusta para el análisis por sus colas pesadas, también especificamos que queremos eliminar los valores faltantes, bambi no los tira por default como statsmodels.

clean_data = data[data['species'] != 'Gentoo'] # solo queremos adelie y chinstrap
model = bmb.Model(
    'body_mass_g ~ species', # también podemos usar la sintaxis de fórmula
    clean_data, # pasamos los datos limpios
    family='t', # podemos usar también Gaussian
    dropna=True # especificamos que queremos retirar los NaN
)
model

Automatically removing 1/220 rows from the dataset.

       Formula: body_mass_g ~ species
        Family: t
          Link: mu = identity
  Observations: 219
        Priors: 
    target = mu
        Common-level effects
            Intercept ~ Normal(mu: 3710.7306, sigma: 1310.4353)
            species ~ Normal(mu: 0.0, sigma: 2351.7068)
        
        Auxiliary parameters
            sigma ~ HalfStudentT(nu: 4.0, sigma: 435.2532)
            nu ~ Gamma(alpha: 2.0, beta: 0.1)

Ahora ajustaremos los datos al modelo con el método fit. Este proceso es costoso, computacionalmente hablando, ya que genera el muestreo de la posterior por el método Montecarlo por cadenas Markov (MCMC). Dependiendo de tu instalación pude que veas algunas advertencias, ignóralas por el momento, se deben a que no instalamos una las dependencias de PyMC.

result = model.fit(chains=4)

Initializing NUTS using jitter+adapt_diag...
C:\Users\User\Documents\coding\curso_python\.venv\Lib\site-packages\pytensor\link\c\cmodule.py:2968: UserWarning: PyTensor could not link to a BLAS installation. Operations that might benefit from BLAS will be severely degraded.
This usually happens when PyTensor is installed via pip. We recommend it be installed via conda/mamba/pixi instead.
Alternatively, you can use an experimental backend such as Numba or JAX that perform their own BLAS optimizations, by setting `pytensor.config.mode == 'NUMBA'` or passing `mode='NUMBA'` when compiling a PyTensor function.
For more options and details see https://pytensor.readthedocs.io/en/latest/troubleshooting.html#how-do-i-configure-test-my-blas-library
  warnings.warn(
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [sigma, nu, Intercept, species]



Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 18 seconds.









Cuando ejecutes el código, observa en el output la columna de «Divergences», deberías observar que las no  encontraron divergencias, lo cual es excelente y nos indica que podemos continuar.
Hagamos diagnóstico de las cadenas, debemos analizar si convergieron adecuadamente. El análisis puede realizarse con arviz.






az.plot_trace(result,);








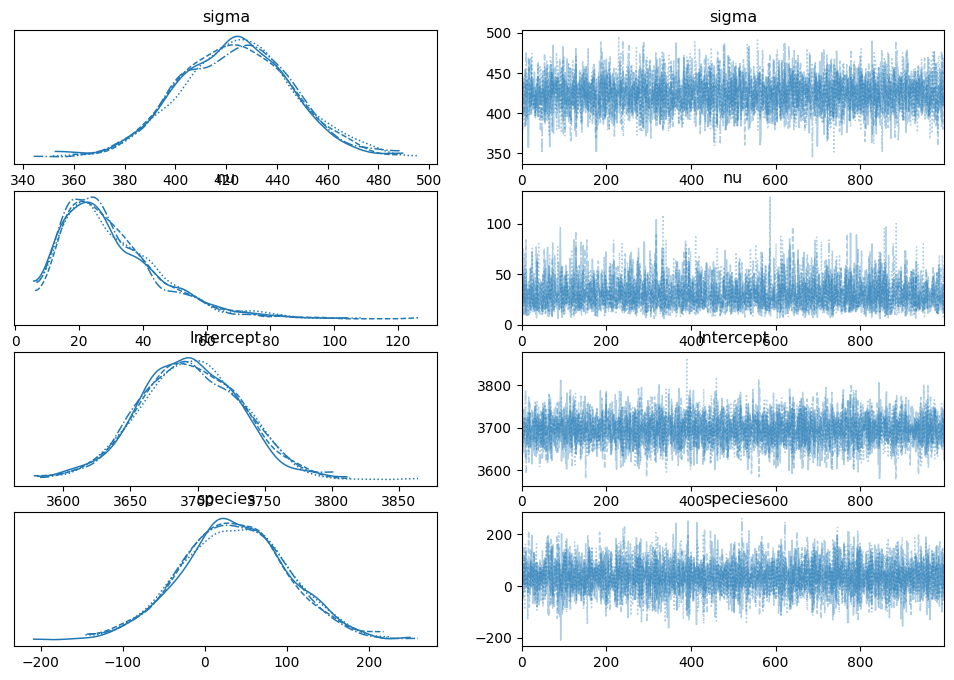
../_images/3c7250ea8a4414b28304d37b265459be49d0c3e515dd09ff899e77fa8b619078.png





Podemos ver que las cadenas parecen haber convergido ya que las trazas tienen forma de «ruido». Ahora podemos analizar los resultados.






az.plot_posterior(result);








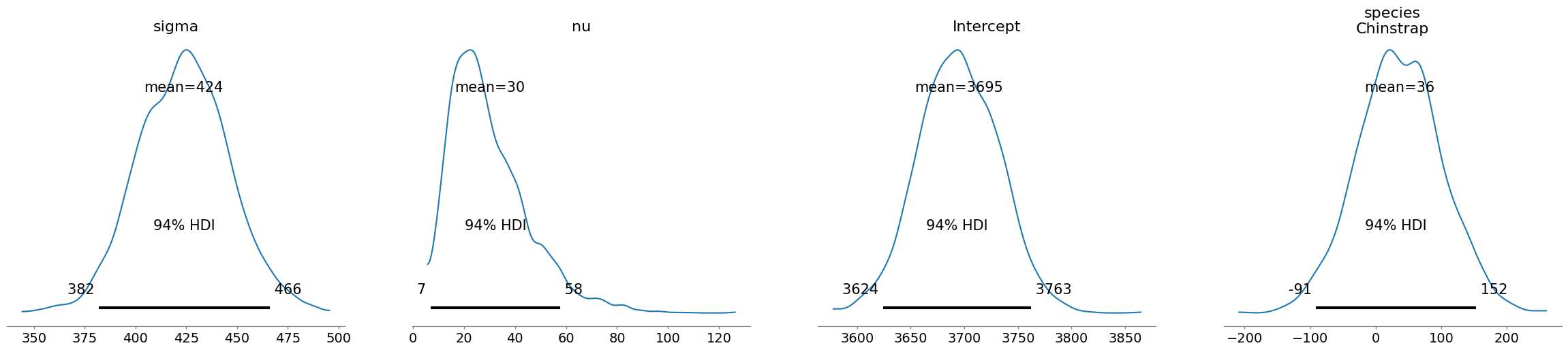
../_images/51e43feafc51b2af4dc9bd53d71b19b2fa0e3f623c85b4fc836dbf14160ab383.png





Esto grafica las posteriores, pero en realidad solo nos interesa el grupo de especie.






az.plot_posterior(
    result, # el objeto resultado de fit
    var_names="species", # el nombre de la variable que nos interesa
    ref_val=0 # el valor de referencia con que queremos comparar.
);








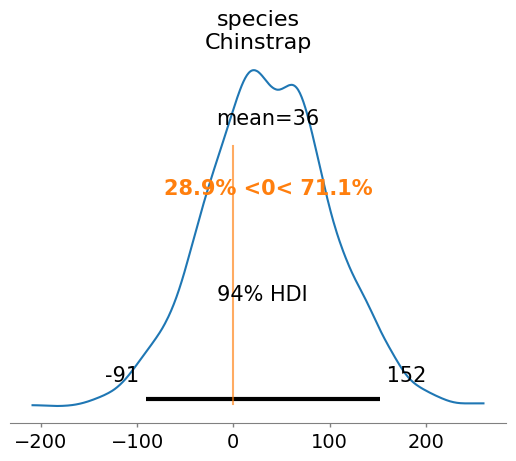
../_images/3ae586c43b1ceddc4857a674e30c1c02157dca92dc889b81b3dd923e4e560062.png





Podemos ver que efectivamente no parece haber diferencia, ya que el intervalo de credibilidad cruza el cero. Veamoslo en forma de tabla.






az.summary(result)













  
    

      
      mean
      sd
      hdi_3%
      hdi_97%
      mcse_mean
      mcse_sd
      ess_bulk
      ess_tail
      r_hat
    

  
  
    

      sigma
      423.677
      22.407
      381.918
      466.119
      0.341
      0.326
      4342.0
      2969.0
      1.0
    

    

      nu
      30.179
      15.369
      7.039
      57.730
      0.227
      0.273
      4302.0
      2709.0
      1.0
    

    

      Intercept
      3694.867
      37.099
      3624.077
      3762.506
      0.494
      0.575
      5610.0
      3009.0
      1.0
    

    

      species[Chinstrap]
      36.213
      64.414
      -91.113
      152.362
      0.776
      1.018
      6893.0
      3302.0
      1.0
    

  







Sigma es la diferencia entre las especies, el intercepto es la media de peso para la especie de referencia (Adelie). Bambi tomó el primer valor como el de referencia, es posible especificar el grupo de referencia pero lo veremos en otra lección, en este caso ambos grupos son adecuados. species[Chinstrap] es la diferencia en el valor del peso para esta especie.


En la tabla también podemos ver el valor \(\hat{R}=1\) en todos los casos, lo que es importante para la confiabilidad de los resultados.


Podemos ver que el intervalo creible  cruza igualmente por el cero, por lo que podemos rechazar la significancia de la diferencia. Pero calculemos el factor bayes, para ello necesitamos muestear el prior y unirlo a nuestro resultado.






prior = model.prior_predictive() # muestreamos el prior
result.extend(prior) # extendemos el resultado para que contenga el prior
az.bayes_factor(result, 'species') # especificamos la variable de interés









Sampling: [Intercept, body_mass_g, nu, sigma, species]
arviz - WARNING - Posterior distribution has {posterior.ndim} dimensions





{'BF10': np.float64(0.003911852822721657),
 'BF01': np.float64(255.63333931981975)}









Podemos ver que tenemos evidencia muy fuerte a favor de la hipótesis nula.






6.3.3. Ejercicio#


    

  1. Ejecuta este método para comparación de medias con tus propios datos.
    2. 

  2. Compara varias cadenas. Ajusta el modelo con diferente número de chains (por ejemplo, 2 o 8) y analiza si afecta el resultado o la convergencia.
    3. 

  3. Realiza la prueba T comparando el peso de acuerdo al sexo.
    4. 







    
    

                

              

              
              
              
              
                
              
            

            
            
              
                



  

  

     Contenido