Medidas de asociación y correlación

5.3. Medidas de asociación y correlación#

En esta libreta analizaremos diferentes medidas de asociación para diferentes conjuntos de datos, tanto numéricos como categóricos.

Consideremos el siguiente flujograma:

        flowchart TD
    A[Dos variables] --> B{¿Tipo?}

    B --> C[Ambas categóricas]
    C --> D{¿Frecuencias esperadas ≥5?}
    D -- Sí --> F[χ² de Pearson]
    D -- No --> G[Test exacto de Fisher]

    F --> Cef[Tamaño del efecto]
    G --> Cef

    Cef --> OR[Odds Ratio]
    Cef --> V[V de Cramer]
    Cef --> Phi[Coeficiente Phi]

    B --> H[Una y Una]
    H --> I[Correlación Rango-Biserial]

    B --> J[Ambas numéricas]
    J --> K{¿Supuestos paramétricos?}
    K -- No --> L[Rho de Spearman]
    K -- No --> M[Tau de Kendall]
    K -- Sí --> N[r de Pearson]

Pese a que este tipo de diagramas son muy limitados, lo uso aquí solo con fines de resumen, no de guía. Siempre decide la prueba adecuada con base en tu contexto científico.

Ten en cuenta que el objetivo no es analizar formalmente los datos sino mostrar cómo se pueden utilizar y ejecutar diferentes formas de asociación.

5.3.1. Librerías y datos#

Utilizaremos datos de un dataset público que puedes encontrar aquí. La ficha técnica del dataset contiene la siguiente información:

  1. Age: Age (in years)

  2. Sex: gender (1 = male; 0 = female)

  3. ChestPain: Chest Pain type .

    • typical angina (all criteria present)

    • atypical angina (two of three criteria satisfied)

    • non-anginal pain (less than one criteria satisfied)

    • asymptomatic (none of the criteria are satisfied)

  4. Restbps: Resting Blood pressure (in mmHg, upon admission to the hospital)

  5. Chol: serum cholesterol in mg/dL

  6. Fbs: fasting blood sugar > 120 mg/dL (likely to be diabetic) 1 = true; 0 = false

  7. RestECG: Resting electrocardiogram results

    • Value 0: normal

    • Value 1: having ST-T wave abnormality (T wave inversions and/or ST elevation or depression of > 0.05 mV)

    • Value 2: showing probable or definite left ventricular hypertrophy by Estes” criteria

  8. MaxHR: Greatest number of beats per minute your heart can possibly reach during all-out strenuous exercise.

  9. Exang: exercise induced angina (1 = yes; 0 = no)

  10. Oldpeak: ST depression induced by exercise relative to rest (in mm, achieved by subtracting the lowest ST segment points during exercise and rest)

  11. Slope: the slope of the peak exercise ST segment, ST-T abnormalities are considered to be a crucial indicator for identifying presence of ischaemia

    • Value 1: upsloping

    • Value 2: flat

    • Value 3: downsloping

  12. Ca: number of major vessels (0-3) colored by fluoroscopy. Major cardial vessels are as goes: aorta, superior vena cava, inferior vena cava, pulmonary artery (oxygen-poor blood –> lungs), pulmonary veins (oxygen-rich blood –> heart), and coronary arteries (supplies blood to heart tissue).

  13. AHD: 0 = normal; 1 = fixed defect (heart tissue can’t absorb thallium both under stress and in rest); 2 = reversible defect (heart tissue is unable to absorb thallium only under the exercise portion of the test)

  14. AHD: 0 = no disease, 1 = disease

import pandas as pd
import scipy.stats as stats
import seaborn as sns
import matplotlib.pyplot as plt

url = 'https://raw.githubusercontent.com/chrisdewa/curso_python/refs/heads/main/bases/Heart_Attack_Data.csv'
df = pd.read_csv(url)
df.head()
age sex cp trestbps chol fbs restecg thalach exang oldpeak slope ca thal target
0 63 1 3 145 233 1 0 150 0 2.3 0 0 1 1
1 37 1 2 130 250 0 1 187 0 3.5 0 0 2 1
2 41 0 1 130 204 0 0 172 0 1.4 2 0 2 1
3 56 1 1 120 236 0 1 178 0 0.8 2 0 2 1
4 57 0 0 120 354 0 1 163 1 0.6 2 0 2 1

Ahora que tenemos los datos, pasemos al análisis.

5.3.2. Dos variables categóricas#

Utilizaremos las variables sex y target. Primero obtengamos la tabla cruzada como se hizo en la lección previa.

tab = pd.crosstab(df['sex'], df['target'])
tab
target 0 1
sex
0 24 72
1 114 93 
tab.shape

(2, 2)

Crearemos una función que realizará la chi cuadrada, obtendrá el OR y su intervalo de confianza e imprimirá en la consola el resultado, además, verificará el supuesto de las frecuencias esperadas.

def chi_cuadrada(tab):
    """Calcula la chi2 y general un reporte de la tabla 2x2"""
    # verificar tipo de tabla
    if tab.shape != (2,2):
        raise ValueError('La tabla debe ser 2x2')
    chi = stats.chi2_contingency(tab)
    OR = stats.contingency.odds_ratio(tab, kind='sample')
    low, high = OR.confidence_interval()
    cumple_frec = bool(v>5 for v in chi.expected_freq.flatten())
    print(f'Resultado de Chi cuadrada: p={chi.pvalue:.1e}, OR={OR.statistic:.2f} (IC 95% {low:.2f} - {high:.2f})')

print('Función definida.')

Función definida.

chi_cuadrada(tab)

Resutado de Chi cuadrada: p=1.9e-06, OR=0.27 (IC 95% 0.16 - 0.47)

Podemos ver que existe una asociación significativa entre la presencia de la enfermedad y el sexo. Como en la tabla está codificado el sexo masculino como 1, curiosamente en estos datos, ser hombre es protector para la enfermedad cardíaca aguda. Además, podemos ver que la p es muy significativa, al igual que el odds ratio.

5.3.2.1. Ejercicio#

  1. Revisa la documentación de las funciones chi2_contingency y odds_ratio.

  2. Ajusta la función para que acepte argumentos adicionales, de forma que podamos calcular intervalos de confianza para diferentes niveles de alfa.

  3. Ajusta la función para el parámetro «kind» de la función odds_ratio, pero primero asegúrate de entender qué hace.

  4. Implementa una función diferente que funcione con la exacta de fisher.

5.3.2.2. Otros tamaños del efecto#

Veremos cómo calcular la V de Cramer y el coeficiente phi.

v = stats.contingency.association(tab, method='cramer')
phi = stats.pearsonr(df['sex'], df['target'])
print(f'V de Cramer: {v}, Phi: {phi.statistic}')

V de Cramer: 0.280936575501767, Phi: -0.28093657550176704

5.3.2.3. Matriz de asociación#

Ahora, podemos utilizar estas métricas, ya que no son exclusivas para datos 2x2, para generar matrices de asociación. Revisando los datos, las variables categóricas son: sex, cp, fbs, restecg, exang, slope, thal, target.

Primero crearemos una función que tome A y B, como series de un dataframe y genere una tabulación cruzada y calcule la V de Cramer.

def cramer_v(a, b):
    tab = pd.crosstab(a, b)
    v = stats.contingency.association(tab)
    return v

cramer_v(df['sex'], df['target'])

0.280936575501767

Ahora utilizaremos la función para generar la matriz de asociación.

categoricas = ['sex', 'cp', 'fbs', 'restecg', 'exang', 'slope', 'thal', 'target']
# utilizaremos la lista para filtrar el dataset y solo seccionar esas columnas.
matriz_asoc = df[categoricas].corr(cramer_v)
matriz_asoc
sex cp fbs restecg exang slope thal target
sex 1.000000 0.150050 0.045032 0.110464 0.141664 0.046257 0.383770 0.280937
cp 0.150050 1.000000 0.113242 0.126437 0.471457 0.213981 0.214676 0.519223
fbs 0.045032 0.113242 1.000000 0.087068 0.025665 0.105514 0.135242 0.028046
restecg 0.110464 0.126437 0.087068 1.000000 0.099106 0.134401 0.076283 0.181878
exang 0.141664 0.471457 0.025665 0.099106 1.000000 0.287995 0.329812 0.436757
slope 0.046257 0.213981 0.105514 0.134401 0.287995 1.000000 0.241295 0.395965
thal 0.383770 0.214676 0.135242 0.076283 0.329812 0.241295 1.000000 0.530594
target 0.280937 0.519223 0.028046 0.181878 0.436757 0.395965 0.530594 1.000000

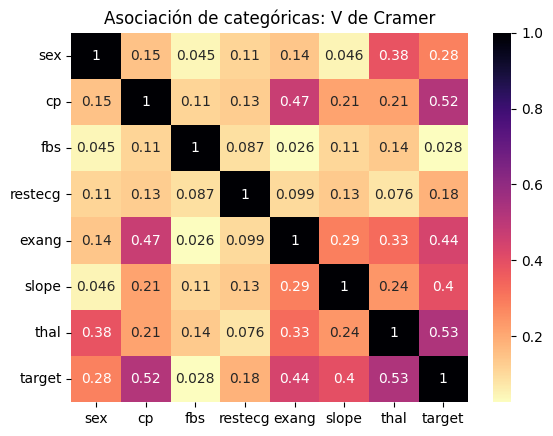
Podemos ahora generar un mapa de calor

sns.heatmap(
    matriz_asoc.round(3), # para mostrar solo 3 decimales
    annot=True,
    cmap='magma_r'
)
plt.title('Asociación de categóricas: V de Cramer')

Text(0.5, 1.0, 'Asociación de categóricas: V de Cramer')
../_images/45acb1a42a5ee68162c4a68fa2009afa1ccda9490df06c75c93c23794923c6ed.png

5.3.3. Una categórica y una numérica#

Para analizar la asociación podemos utilizar la correlación punto biserial, que está implementada directamente en scipy. Utilicemos target y age.

stats.pointbiserialr(df['target'], df['age']) # x debe ser cat, y num

SignificanceResult(statistic=np.float64(-0.22543871587483735), pvalue=np.float64(7.524801303442137e-05))

5.3.4. Dos numéricas#

Ahora veamos cómo ejecutar las diferentes correlaciones.

5.3.4.1. Pearson#

stats.pearsonr(df['trestbps'], df['chol'])

PearsonRResult(statistic=np.float64(0.12317420653239072), pvalue=np.float64(0.03208205361087139))

5.3.4.2. Spearman#

stats.spearmanr(df['trestbps'], df['chol'])

SignificanceResult(statistic=np.float64(0.12656163345944624), pvalue=np.float64(0.027608539162108585))

5.3.4.3. Kendall Tau#

5.3.4.3.1. Variante B#

stats.kendalltau(df['trestbps'], df['chol'], variant='b')

SignificanceResult(statistic=np.float64(0.08647408139339434), pvalue=np.float64(0.029128580856773133))

5.3.4.3.2. Variante C#

stats.kendalltau(df['trestbps'], df['chol'], variant='c')

SignificanceResult(statistic=np.float64(0.08526124889716695), pvalue=np.float64(0.029128580856773133))

5.3.5. Ejercicios#

  1. Gráfica las correlaciones.

  2. Continúa explorando los datos presentados.

  3. Revisa la página del dataset: https://www.kaggle.com/datasets/pritsheta/heart-attack/data.

  4. Revisa el código de otros para ver qué tipos de análisis utilizan.

  5. Revisa estas dos libretas en particular:

Contenido