Actualización de una Proporción

6.1. Actualización de una Proporción#

En esta libreta exploraremos cómo podemos realizar una actualización bayesiana de la estimación de una proporción en estudios seriados.

6.1.1. Librerías#

import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
print('Librerías importadas')

Librerías importadas

Tomaremos como base el siguiente paper.

Fombonne E, Marcin C, Manero AC, Bruno R, Diaz C, Villalobos M, Ramsay K, Nealy B. Prevalence of Autism Spectrum Disorders in Guanajuato, Mexico: The Leon survey. J Autism Dev Disord. 2016 May;46(5):1669-85. doi: 10.1007/s10803-016-2696-6. PMID: 26797939.

Se describe que de la muestra de 432 niños, 31 presentaron autismo, una proporción de 0.7%; aunque en el estudio se estima la prevalencia en 0.87% este número se obtuvo por simulación, así que tomaremos el valor empírico.

n = 432
casos = 31
prop = casos/n
print(f'Prevalencia: {prop:.2%}')

Prevalencia: 7.18%

Podemos modelar la proporción con la distribución beta, utilizando scipy. La distribución Beta se define: \(~Beta(\alpha; \beta)\), donde alfa es el número de casos positivos y beta los negativos, es decir \(\beta = n - \alpha\).

# función helper para no repetir el código muchas veces.

def plot_beta(alfa, beta, label=None):
    """Esta función grafica la distribución con los parámetros dados"""
    # obtenemos la densidad en el intervalo 0,1
    dist = stats.beta(alfa, beta)
    y = dist.pdf(x)
    plt.plot(x, y, label=label)
    moda = (alfa - 1) / (alfa + beta - 2)
    plt.axvline(moda, ls=':', color='k', alpha=0.3, label=f'moda={moda:.2f}')
    plt.title(r'Distribución del parámetro $\theta$')
    plt.xlabel('x')
    plt.ylabel('Densidad')
    plt.legend()


# x es un vector unidimensional del 0 al 0.3 con 1000 elementos.
x = np.linspace(0, 0.3, 1000) # 1000 es solo para la resolución
alfa = casos
beta = n- alfa

plot_beta(alfa, beta, label='Estudio original')
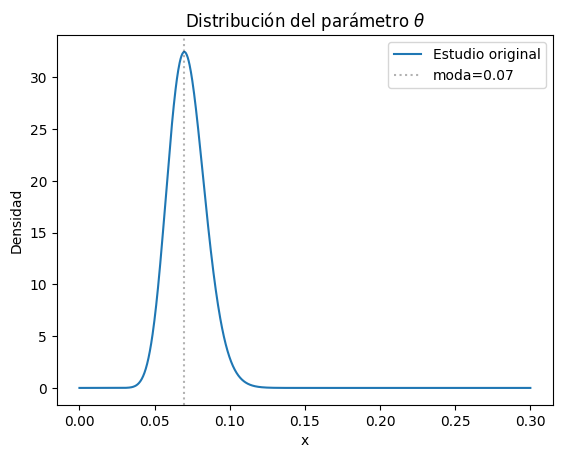
../_images/6c965aff2717fdfdfa7299cddcac09f92ed2055f1234e337a94625d19aa09207.png

Ahora supongamos que un estudio reciente encontró que en una cohorte de 157 niños, 15 tenían autismo. Podemos realizar una actualización bayesiana de la siguiente manera.

alfa2 = alfa + 15 # agregamos al parámetro alfa nuestro 
beta2 = n + 157 - alfa2

plot_beta(alfa, beta, label='Prior empírico (estudio 1)')
plot_beta(alfa2, beta2, label='Posterior (con estudio 2)')
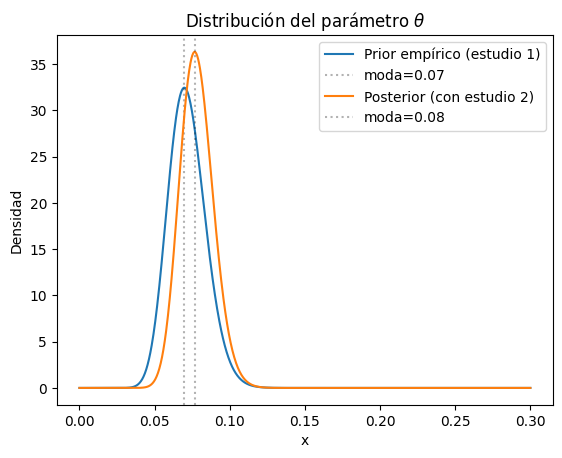
../_images/a6f5bd59ed335c21b9af1864a3b03949bfefd659c7320494e53800f4410affda.png

La proporción del estudio de replicación fue \(15/157 = 0.0955\), pero al realizar la actualización bayesiana con la distribución Beta, el nuevo máximo a posteriori para la prevalencia es \(MAP ~ Beta(\alpha_2, \beta_2) \approx 0.08\), MAP es «maximo a posteriori» y para la distribución beta es la moda, que cuando alfa y beta son mayores de 1, se define como:

\[ moda = \frac{\alpha - 1}{\alpha + \beta -2} \]

6.1.2. Ejercicios#

  1. Prueba la actualización con diferentes valores de alfa y beta.

  2. Ejecuta el análisis con datos que sean de tu interés. Puedes utilizar este método para combinar diferentes fuentes de información.

  3. Revisa la distribución beta y ajusta la función plot_beta para contemplar otros casos de alfa y beta para la moda.

  4. Ajusta el eje x de la gráfica para que cubra el 99% de probabilidad de la distribución (por ejemplo, usando ppf(0.001) y ppf(0.999)), y compara cómo cambia la visualización con respecto al rango fijo original.

Contenido