5.7. Modelos Mixtos#
En la libreta previa exploramos cómo realizar un análisis de varianza de medidas repetidas en el dataset de sleepstudy, y comentamos que este dataset es muy utilizado para ejemplificar el uso y ventajas de los modelos mixtos o jerárquicos.
5.7.1. Librerías y datos#
import pandas as pd
import scipy.stats as stats
import numpy as np
import seaborn as sns
import statsmodels.api as sm
# !pip install pingouin -q # quita este comentario si estás en colab
import pingouin as pg
dataset = sm.datasets.get_rdataset('sleepstudy', package='lme4')
print("Librerías importadas y datset descargado")
Librerías importadas y datset descargado
Exploremos qué información adicional nos da statsmodels sobre este dataset.
dataset.title
'Reaction times in a sleep deprivation study'
dataset.package
'lme4'
.package nos dice de qué paquete de R se tomó el dataset, en este caso LME4.
También podemos ver la documentación propia de R para este dataset.
print(dataset.__doc__)
.. container::
.. container::
========== ===============
sleepstudy R Documentation
========== ===============
.. rubric:: Reaction times in a sleep deprivation study
:name: reaction-times-in-a-sleep-deprivation-study
.. rubric:: Description
:name: description
The average reaction time per day (in milliseconds) for subjects
in a sleep deprivation study.
Days 0-1 were adaptation and training (T1/T2), day 2 was baseline
(B); sleep deprivation started after day 2.
.. rubric:: Format
:name: format
A data frame with 180 observations on the following 3 variables.
``Reaction``
Average reaction time (ms)
``Days``
Number of days of sleep deprivation
``Subject``
Subject number on which the observation was made.
.. rubric:: Details
:name: details
These data are from the study described in Belenky et al. (2003),
for the most sleep-deprived group (3 hours time-in-bed) and for
the first 10 days of the study, up to the recovery period. The
original study analyzed speed (1/(reaction time)) and treated day
as a categorical rather than a continuous predictor.
.. rubric:: References
:name: references
Gregory Belenky, Nancy J. Wesensten, David R. Thorne, Maria L.
Thomas, Helen C. Sing, Daniel P. Redmond, Michael B. Russo and
Thomas J. Balkin (2003) Patterns of performance degradation and
restoration during sleep restriction and subsequent recovery: a
sleep dose-response study. *Journal of Sleep Research* **12**,
1–12.
.. rubric:: Examples
:name: examples
.. code:: R
str(sleepstudy)
require(lattice)
xyplot(Reaction ~ Days | Subject, sleepstudy, type = c("g","p","r"),
index = function(x,y) coef(lm(y ~ x))[1],
xlab = "Days of sleep deprivation",
ylab = "Average reaction time (ms)", aspect = "xy")
(fm1 <- lmer(Reaction ~ Days + (Days|Subject), sleepstudy, subset=Days>=2))
## independent model
(fm2 <- lmer(Reaction ~ Days + (1|Subject) + (0+Days|Subject), sleepstudy, subset=Days>=2))
5.7.1.1. Datos#
Para acceder a los datos utilizamos el atributo data.
data = dataset.data
data.head()
| Reaction | Days | Subject | |
|---|---|---|---|
| 0 | 249.5600 | 0 | 308 |
| 1 | 258.7047 | 1 | 308 |
| 2 | 250.8006 | 2 | 308 |
| 3 | 321.4398 | 3 | 308 |
| 4 | 356.8519 | 4 | 308 |
5.7.2. Modelo#
Modelaremos la relación entre los días de deprivación de sueño y el tiempo de reacción permitiendo una pendiente aleatoria para cada sujeto a lo largo del tiempo.
5.7.2.1. Interceptos aleatorios#
model1 = sm.MixedLM.from_formula(
'Reaction ~ Days',
data=data,
groups='Subject', # intercepto aleatorio
)
result1 = model1.fit()
print(result1.summary())
Mixed Linear Model Regression Results
==========================================================
Model: MixedLM Dependent Variable: Reaction
No. Observations: 180 Method: REML
No. Groups: 18 Scale: 960.4568
Min. group size: 10 Log-Likelihood: -893.2325
Max. group size: 10 Converged: Yes
Mean group size: 10.0
----------------------------------------------------------
Coef. Std.Err. z P>|z| [0.025 0.975]
----------------------------------------------------------
Intercept 251.405 9.747 25.794 0.000 232.302 270.508
Days 10.467 0.804 13.015 0.000 8.891 12.044
Subject Var 1378.176 17.156
==========================================================
En este modelo estamos permitiendo que cada sujeto varíe su intercepto, es decir, ajustamos el modelo para el tiempo de reacción de cada sujeto al momento cero.
Si analizamos lo resultados, vemos que el intercepto es 251.405, este es el promedio del tiempo de reacción de los sujetos antes de la deprivación de sueño, es decir al momento cero. El coeficiente de Days es 10.467 es decir, que en promedio, cada día de deprivación, aumentó el tiempo de reacción en 10 ms.
Observa que la varianza de cada sujeto es de 1378.176, la desviación estándar sería su raíz 37.123.
En el output de summary puedes ver también un rubro de scale que se refiere a la varianza del error del modelo.
Este modelo, sin embargo, no considera que cada sujeto responde de forma diferente a la deprivación, algunos sujetos parecen aumentar más o menos su tiempo de reacción conforme pasan los días. Veamos la siguiente figura.
5.7.2.2. Visualización#
sns.lmplot(
data,
x='Days',
y='Reaction',
col='Subject',
col_wrap=6,
aspect=0.7,
)
<seaborn.axisgrid.FacetGrid at 0x1ec5d1a9d30>
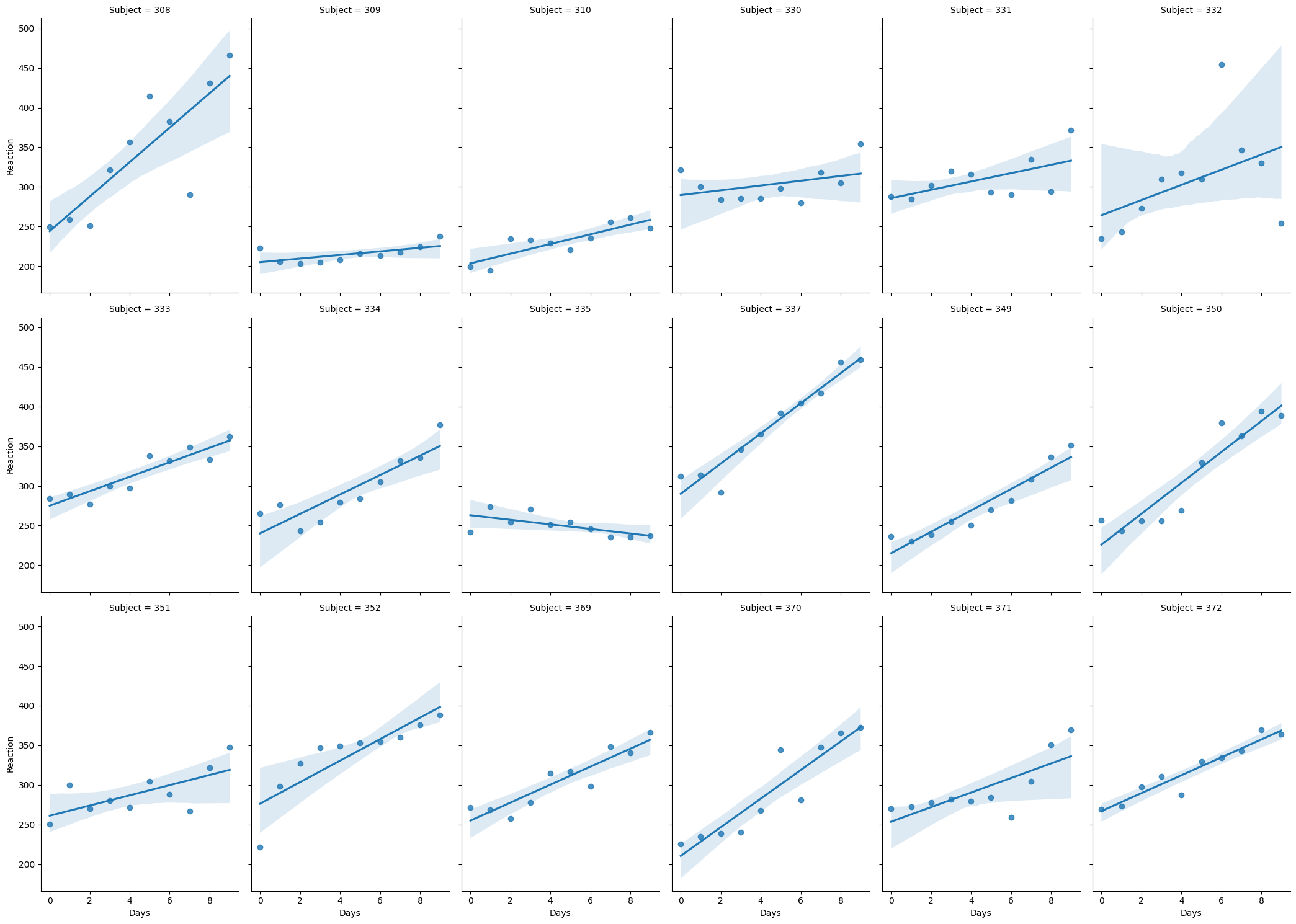
5.7.2.3. Pendiente aleatoria#
Para poder contemplar la pendiente de cada sujeto en el modelo, debemos agregar una pendiente aleatoria, en statsmodels se ve así:
model2 = sm.MixedLM.from_formula(
'Reaction ~ Days',
data=data,
groups='Subject', # intercepto aleatorio
re_formula='~ Days', # pendiente aleatoria (Days|Subject)
)
result2 = model2.fit()
print(result2.summary())
Mixed Linear Model Regression Results
================================================================
Model: MixedLM Dependent Variable: Reaction
No. Observations: 180 Method: REML
No. Groups: 18 Scale: 654.9405
Min. group size: 10 Log-Likelihood: -871.8141
Max. group size: 10 Converged: Yes
Mean group size: 10.0
----------------------------------------------------------------
Coef. Std.Err. z P>|z| [0.025 0.975]
----------------------------------------------------------------
Intercept 251.405 6.825 36.838 0.000 238.029 264.781
Days 10.467 1.546 6.771 0.000 7.438 13.497
Subject Var 612.096 11.881
Subject x Days Cov 9.605 1.821
Days Var 35.072 0.610
================================================================
Analicemos el resultado, en primer lugar destaca que disminuyó scale lo que quiere decir que el modelo tiene un error más pequeño y tenemos dos nuevos componentes en la matriz de varianzas-covarianzas: Subject x Days Cov y Days Var.
Subject x Days Cov: Es la covarianza del efecto de los días sobre cada sujeto. Es positiva, lo que nos indica que los sujetos que comienzan con más tiempo de reacción tienden a aumentar más su tiempo de reacción conforme pasan los días. Podemos incluso utilizar la fórmula de la correlación para convertir este valor en una forma más interpretable.
Para resolverlo, ya tenemos la varianza del sujeto y la varianza de días, así que podemos utilizar el siguiente código:
result2.cov_re # matriz de covarianza
| Subject | Days | |
|---|---|---|
| Subject | 612.096487 | 9.604599 |
| Days | 9.604599 | 35.071623 |
cov = result2.cov_re.loc['Subject', 'Days']
var_subj = result2.cov_re.loc['Subject', 'Subject']
var_days = result2.cov_re.loc['Days', 'Days']
corr = cov / (np.sqrt(var_subj) * np.sqrt(var_days))
print(corr.round(3))
0.066
La correlación es pequeña, pero positiva. Una correlación cercana a cero indica que la variabilidad en el intercepto de los sujetos no está fuertemente relacionada con su sensibilidad al número de días de privación del sueño.
Este modelo contempla no solo el cambio del tiempo de reacción en el tiempo, sino que considera la variabilidad de cada sujeto.
5.7.3. GEE#
Los modelos de efectos mixtos son poderosos, robustos y estables para analizar datos longitudinales, jerárquicos o agrupados y el resultado se enfoca en los individuos, pero si quisiéramos conocer el efecto poblacional de la deprivación del sueño, el modelo de elección serían las Ecuaciones de estimación generalizadas (GEE).
model3 = sm.GEE.from_formula(
'Reaction ~ Days',
data=data,
groups='Subject'
)
result3 = model3.fit()
print(result3.summary())
GEE Regression Results
===================================================================================
Dep. Variable: Reaction No. Observations: 180
Model: GEE No. clusters: 18
Method: Generalized Min. cluster size: 10
Estimating Equations Max. cluster size: 10
Family: Gaussian Mean cluster size: 10.0
Dependence structure: Independence Num. iterations: 2
Date: Tue, 22 Jul 2025 Scale: 2276.694
Covariance type: robust Time: 08:10:36
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 251.4051 6.632 37.906 0.000 238.406 264.404
Days 10.4673 1.502 6.968 0.000 7.523 13.412
==============================================================================
Skew: 0.0147 Kurtosis: 0.3867
Centered skew: 0.2144 Centered kurtosis: 2.3434
==============================================================================
A diferencia de los modelos mixtos, GEE no modela la variabilidad entre sujetos, sino que corrige la estimación de los efectos fijos teniendo en cuenta la correlación entre medidas repetidas. En el modelo 3 se usó la estructura de correlación independiente (por defecto), que no siempre es adecuada para datos longitudinales. Por eso, en el modelo 4 probamos una estructura exchangeable, que asume una correlación constante entre las observaciones de cada sujeto.
from statsmodels.genmod.cov_struct import Exchangeable
model4 = sm.GEE.from_formula(
'Reaction ~ Days',
data=data,
groups='Subject',
cov_struct=Exchangeable()
)
result4 = model4.fit()
print(result4.summary())
GEE Regression Results
===================================================================================
Dep. Variable: Reaction No. Observations: 180
Model: GEE No. clusters: 18
Method: Generalized Min. cluster size: 10
Estimating Equations Max. cluster size: 10
Family: Gaussian Mean cluster size: 10.0
Dependence structure: Exchangeable Num. iterations: 2
Date: Tue, 22 Jul 2025 Scale: 2276.694
Covariance type: robust Time: 08:15:51
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 251.4051 6.632 37.906 0.000 238.406 264.404
Days 10.4673 1.502 6.968 0.000 7.523 13.412
==============================================================================
Skew: 0.0147 Kurtosis: 0.3867
Centered skew: 0.2144 Centered kurtosis: 2.3434
==============================================================================
En este caso, el resultado del modelo no cambia al modificar la estructura de correlación, ya que solo hay una observación por día por sujeto. Esto impide estimar de forma significativa la correlación entre medidas dentro de cada sujeto. Aun así, es buena práctica especificar una estructura de covarianza apropiada cuando se trabaja con datos longitudinales.
5.7.4. Ejercicio#
Aplica lo aprendido en con tus propios datos.
Busca el dataset
pbcdesurvival. Lee su documentación y analízalo con las herramientas que aprendiste.

